In order to calculate the effect of tree shading on a roof, we need to know: The first two calculations are simple trig, the last can be obtained from tables.

The case of Lakeside Court

(see crude drawing at bottom)

Calculating the shadow of a tree on a roof (Assuming a pyramidal shaped tree)

Tree Height 50
Tree distance 25
Roof Height 10
The Noon Angle is merely the Acrtan of the differences in height/ distance= arc tan 1.01 or in degrees 58.
Unfortunately, the tree is not pyramidal, but branches out. As far as we can tell, the maximum extent is about 25 feet up and stick out about 13 feet. This leads to a shadow angle of about 52 degrees.

Corner angle of shade

Distance to tree 25
Distance from N-S 15
Artan 0.54 or in degrees 31 (from South, or 149 degrees)

Elevation angle at the corner is
tree height 35
tree distance 29
Arctan 0.80 or an elevation in degrees of 40

Conclusion:

From the following tables, we can see that from late March to mid September, the sun is above the critical value of 50 degrees. For late September until the leaves fall, there will be some shading in the late morning and until a little after noon.

To make these estimates more precise we need to confirm the height of the tree and examine its shape more carefully. It seems that with more precise measurements, we probably should not plan on using the garage.

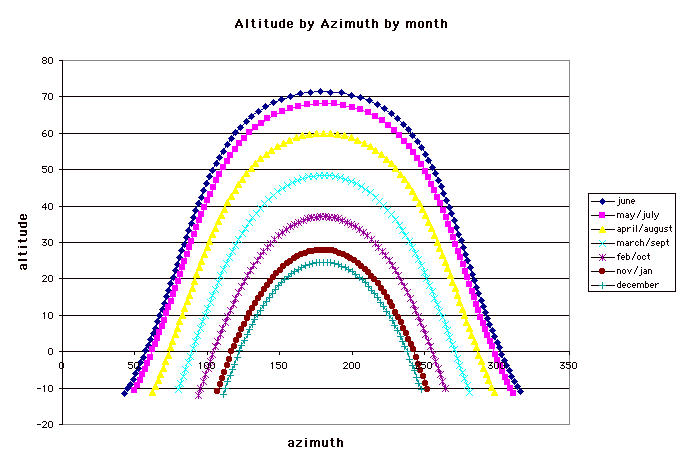
The best way to understand the solar angles is to consider solar elevation by solar azimuth. These are derived from hourly tables of azimuths and elevations. Elevations by angle

The solar elevations by hour by month are taken from tables: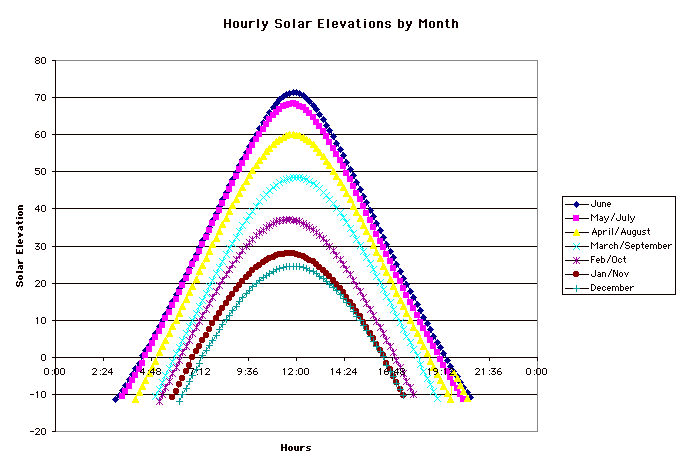Hourly Solar Elevations by Month
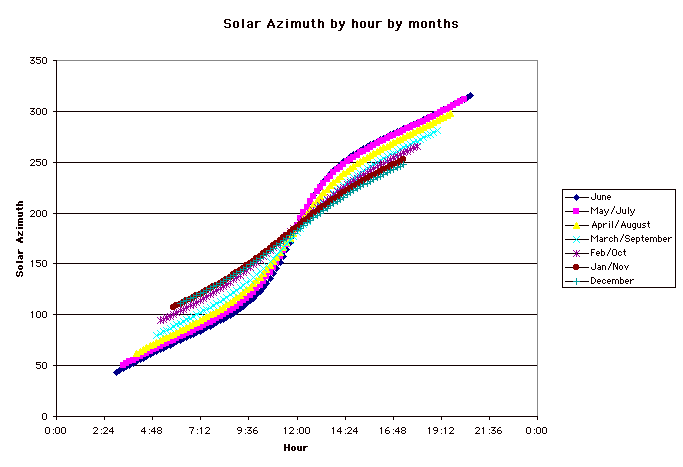
And the solar azimuths by hour and month also are tabled: Hourly Solar Azimuths by Month

The basic assumptions are shown as below (but not to scale):
calculations